Alla scoperta di bboot, il package R che implementa il block stationary bootstrap
bboot è disponibile al seguente repository GitHub: https://github.com/lamferzon/bboot ed è ben documentato per assicurare un più vasto utilizzo…
Alla scoperta di bboot, il package R che implementa il block stationary bootstrap
Una delle tecniche di ricampionamento con reimmissione più utilizzate per fare inferenza statistica su un parametro è il metodo bootstrap. Un importante limite di questa metodologia è che non può essere utilizzata ogniqualvolta si ha un campione y = [y(1), y(2), …, y(n)] di numerosità n i cui dati risultano essere correlati tra di loro. Infatti, il campionamento singolo da y per ottenere l’i-esimo campione bootstrap y(i)* = [y(i,1)*, y(i,2)*, …, y(i,N)*] di lunghezza N, comporta la rottura del legame esistente tra osservazioni correlate quando i dati non sono indipendenti. Per ovviare a questo problema, in letteratura è stata proposta la tecnica block stationary bootstrap (BSB), un’estensione della metodologia base che campiona da y a blocchi piuttosto che lavorando sulle singole unità.
Il principio su cui il BSB si basa è il seguente: dopo aver scelto casualmente idx0, ossia una delle n osservazioni del campione y, vengono selezionate le (L-1) osservazioni consecutive a idx(0) così da creare il blocco [idx(0), idx(1), idx(2), …, idx(L-1)]; questa procedura viene iterata finché l’i-esimo campione bootstrap y(i)*, che si ottiene accostando i blocchi che via via vengono creati durante l’esecuzione dell’algoritmo, raggiunge la numerosità N desiderata, la quale può essere sia maggiore sia minore di n. La lunghezza L dei blocchi viene scelta casualmente a ogni j-esima iterazione (per iterazione si intende il passo in cui viene creato un blocco); di norma la distribuzione di questo parametro è poissoniana. Il numero di iterazioni non è determinabile a priori perché dipende dalla lunghezza aleatoria dei blocchi. L’algoritmo viene ripetuto K volte, così da ottenere in output K campioni bootstrap Y = [y(1)* y(2)*… y(i)*… y(K-1)* y(K)*]. La Figura 1 riporta un esempio esemplificativo del funzionamento del BSB per la creazione di un singolo campione bootstrap con 4 iterazioni.
Figura 1: schematizzazione del principio di funzionamento del block stationary bootstrap. In questo caso si considera un singolo campione bootstrap y(i)*, quindi questa procedura deve essere ripetuta K volte se si desidera ottenere più di un campione.

Il block stationary bootstrap risulta essere particolarmente indicato per la simulazione di serie storiche stazionarie, ove le loro statistiche non dipendendo dal tempo t, ma dalla distanza temporale tra le osservazioni che costituiscono y. Quindi, se L viene scelto in modo tale che ogni singolo blocco sia sufficientemente esaustivo per descrivere l’autocorrelazione esistente nei dati, allora i blocchi possono essere liberamente accostati per ottenere una serie storica y(i)* che rispecchi le caratteristiche statistiche di quella originale.
Per MATLAB è già disponibile una funzione che implementa il BSB (stationaryBB, scaricabile tramite il MATLAB file transfer), mentre per R ancora non esiste, pertanto abbiamo deciso di realizzare bboot, un package avente il compito di fornire ai programmatori R una soluzione pronta all’uso del block stationary bootstrap tramite l’omonima funzione blockboot(). La necessità di questo package nasce dal progetto AgrImOnIA. Data la serie storica di un inquinante, volevamo simulare i dati mancanti tramite il BSB, così da misurare le prestazioni in validazione dei modelli ARIMA utilizzati per la ricostruzione dei missing values. I dati mancanti sono dovuti ai malfunzionamenti delle centraline adibite alla misurazione delle concentrazioni di inquinanti nell’aria. Prima che un guasto venga risolto possono passare alcuni giorni, di conseguenza i missing values occorrono nelle serie storiche non in maniera isolata, ma a blocchi; da ciò deriva la necessità di utilizzare il block stationary bootstrap piuttosto che la tecnica base di ricampionamento.
La funzione MATLAB che implementa il BSB è implementata come ricampionamento con ripetizione, ovvero i blocchi non sono disgiunti tra di loro, un comportamento indesiderato per quello che è il fine di utilizzo del block stationary bootstrap per questo caso specifico. Pertanto, blockboot() è stata implementata come ricampionamento senza ripetizione, ovvero la selezione dei blocchi è tale che all’iterazione j-esima non possa essere scelto un blocco contenente indici di osservazioni che sono stati precedentemente scelti. Ovviamente, questo comportamento si verifica solo quando N, ossia la lunghezza del singolo campione bootstrap y(i)*, è minore di n, cioè la lunghezza del campione originale; infatti, se N è maggiore di n, allora il vincolo di non sovrapposizione deve essere rilassato affinché y* raggiunga la lunghezza desiderata avendo a disposizione solo n dati (è necessario scegliere delle osservazioni che sono state precedentemente selezionate).
In questo momento bboot non è ancora disponibile su CRAN, l’archivio ufficiale di R, tuttavia è possibile consultare il seguente repository GitHub:
https://github.com/lamferzon/bboot
Per l’installazione è sufficiente eseguire in R i seguenti comandi:
>> devtools::install_github(“lamferzon/block-bootstrap-for-R”)
>> library(bboot)
Il package è ben documentato per assicurare un più vasto utilizzo, pertanto si rimanda all’help di blockboot() per avere ulteriori informazioni in merito ai parametri della funzione e al suo funzionamento. Degna di nota la possibilità di ricevere in output non sono gli indici delle osservazioni che non sono state campionate, ma anche un summary contenente, per ognuna delle simulazioni, il valore di alcuni parametri prestazionali:
– num. iterations: numero di iterazioni dell’algoritmo necessarie per ottenere una serie storica simulata di lunghezza N;
– num. blocks: numero di blocchi creati;
– mean blocks length: lunghezza media dei blocchi; è bene notare che di default la lunghezza di ogni singolo blocco viene scelta casualmente da una distribuzione poissoniana di parametro λ (da specificare in input);
– num. out-of-indexes: numero di iterazioni (perse) in cui è stato selezionato un blocco contenente osservazioni i cui indici superano quello dell’ultimo dato nel campione y;
– num. rejected indexes: numero di interazioni (perse) in cui è stato selezionato un blocco contenente osservazioni i cui indici sono già stati selezionati;
– execution time: tempo necessario per generare y*.
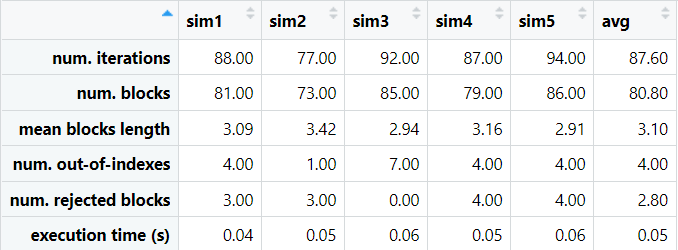
La Tabella 1 riporta un esempio di summary con blockboot() configurato nel seguente modo: K = 5, L = 3, distribuzione poissoniana e N = 250 < n. Consideriamo, per esempio, la prima simulazione (sim1); per generare y(1)* sono state necessarie 88 iterazioni, 81 hanno portato all’effettiva selezione di un blocco, mentre nelle restanti 7 i blocchi scelti sono stati scartati perché contenenti indici o fuori limite massimo (4) oppure perché già presenti in blocchi creati precedentemente (3).
Tabella 1: output di blockboot() per un esempio con K = 5, L = 3, distribuzione poissoniana e N = 250 < n.
Di blockboot() è stata svolta anche un’analisi prestazionale. I grafici in Figura 2 e 3 mostrano l’andamento della lunghezza media dei blocchi e del tempo di esecuzione in funzione del rapporto N/n in due casi:
-
blocks rejection disattivata per N maggiore di n (Figura 2): accettazione di blocchi il cui indice iniziale è già stato selezionato come primo indice per blocchi che già sono stati creati.
-
blocks rejection attivata per N maggiore di n (Figura 3): rifiuto di blocchi il cui indice iniziale è già stato selezionato come primo indice per blocchi che già sono stati creati.
L’analisi è stata svolta con K = 5, L = 3 e distribuzione poissoniana delle lunghezze L.
Nel primo caso, è possibile notare che il tempo di esecuzione (punti in arancione nel grafico) aumenta esponenzialmente all’avvicinarsi a 1 del rapporto N/n, ossia quando si vuole generare una simulazione la cui lunghezza coincide esattamente con quella del campione originale; i blocchi non possono sovrapporsi, pertanto ogni singolo dato di y dev’essere scelto una e una sola volta affinché N sia uguale a n. Il numero di indici che può essere scelto come idx(0) alla j-esima iterazione diventa sempre più piccolo all’aumentare di j e la lunghezza L (scelta casualmente) deve essere tale da non provocare una sovrapposizione con i blocchi che già sono stati creati, quindi il numero di iterazioni perse diventa sempre più grande, provocando pertanto un aumento del tempo di esecuzione; nonostante ciò, l’algoritmo arriva a convergenza in un tempo finito. Per N maggiore di n, invece, non c’è alcun vincolo sulla scelta del primo indice idx(0) perché il blocks rejection è disattivato. A ogni iterazione le osservazioni sono sempre tutte disponibili, pertanto non possono verificarsi rejected indexes; ciò si traduce in un tempo di esecuzione prossimo a zero. Per quanto riguarda la lunghezza media dei blocchi (punti in verde nel grafico), essa risulta essere sempre vicina alla scelta L tranne per N prossimo a n, situazione in cui la lunghezza dei blocchi diventa sempre più piccola all’aumentare di j: la probabilità che molti dei dati nelle vicinanze di idx(0) alla j-esima iterazione siano già stati inseriti in blocchi che già sono stati creati è elevata, quindi è necessario che L sia piccolo (o addirittura uguale a 1) affinché il blocco corrente non venga rifiutato.
Infine, per il secondo caso valgono in generale le considerazioni fatte precedentemente, ma c’è una sostanziale differenza: per N maggiore di n il tempo di esecuzione aumenta all’aumentare del rapporto N/n. Questo comportamento è causato dall’impossibilità di scegliere come primo indice idx0 alla j-esima iterazione un’osservazione che è già primo indice di un blocco che è già stato generato in una delle iterazioni precedenti dell’algoritmo (il blocks rejection è attivato), di conseguenza il numero di osservazioni disponibili diminuisce progressivamente all’aumentare di j, provocando un aumento del numero di iterazioni perse e quindi del tempo necessario per generare una delle k simulazioni y(i)* di lunghezza N.

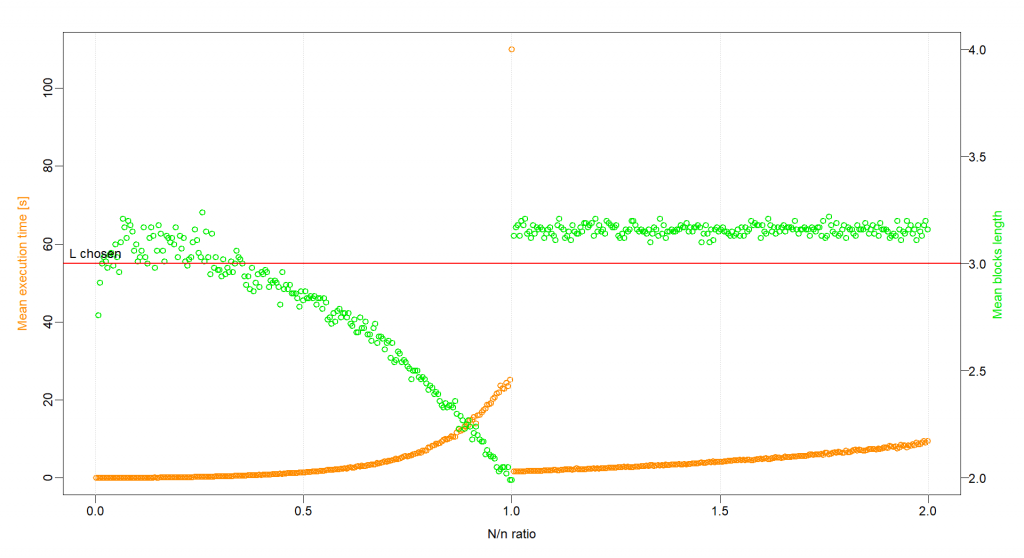
Figura 2: andamento del tempo di esecuzione medio in secondi (mean execution time, punti in arancione) e della lunghezza media dei blocchi (punti in verde) in funzione del rapporto N/n con blocks rejection attivata.
Figura 3: andamento del tempo di esecuzione medio in secondi (mean execution time, punti in arancione) e della lunghezza media dei blocchi (punti in verde) in funzione del rapporto N/n con blocks rejection disattivata.
Dott. Lorenzo Leoni
Studente magistrale di Ingegneria Informatica, indirizzo DSDE
Università degli Studi di Bergamo
l.leoni2@studenti.unibg.it